Voornamendrift (8)

Door Gerrit Bloothooft

Wanneer een nieuwe voornaam meerdere keren wordt gegeven is dat veel interessanter dan de unieke, eenmalige naam. In het laatste geval kan er sprake zijn van een creatieve opwelling, een gebrek aan kennis van spelling, of simpelweg een typefout. Maar een herhaling, dat dezelfde gedachte gedeeld wordt door meerdere ouders, is opmerkelijk. Dat kan ons iets leren over toeval of hoe namen zich verspreiden.

Stel dat er een nieuwe voornaam bedacht is door ouders, of in ieder geval nieuw geïntroduceerd is in Nederland. Hoe lang duurt het voordat andere ouders die naam ook kiezen? Voor onze gegevens uit de Gemeentelijke Basisadministratie kunnen we voor namen die na 1920 voor het eerst zijn gegeven wel zeggen dat ze nieuw zijn. Daarnaast moeten we een nieuwe naam voldoende tijd geven tot de tweede naamgeving. Daarom beschouwen we alleen namen die in de periode 1920-1960 voor het eerst gegeven zijn, want dan is er minimaal 54 jaar beschikbaar (tot onze selectie van 2014) voor het verschijnen van de tweede naamgeving. Het is voor deze analyses noodzakelijk om over meer dan een eeuw te weten welke voornamen gegeven zijn, en het is geweldig en uitzonderlijk dat we dat voor Nederland kunnen doen.

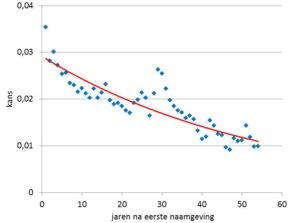
We bekijken eerst de namen die precies twee keer gegeven zijn, en niet vaker. In figuur 1 staat de kans op de tijd tussen de eerste en tweede naamgeving. Die kans neemt heel  geleidelijk exponentieel af van 3,5% naar 1% (formule p_1,2(j) = 0,03*(0,97)^j  met j = aantal  jaren) met een opleving rond 30 jaar. Dat betekent dat de tweede naamgeving niet helemaal onafhankelijk is van de eerste, want dan zou de kans constant zijn. Vernoeming creëert afhankelijkheid en daar is rond 30 jaar inderdaad sprake van, zoals de vernoeming van vader op zoon of moeder op dochter bij Euwout en Tieberdina.

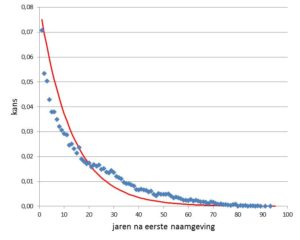
Meer algemeen kun je kijken naar de tijd tussen de eerste en tweede naamgeving van een nieuwe naam, ongeacht hoeveel kinderen daarna de naam nog zullen krijgen. Je kunt redeneren dat die kinderen geen invloed kunnen hebben, want ze zijn nog niet geboren. Als we de eis van tweemaligheid loslaten staat het resultaat in figuur 2.

De hoogste kans (7%) is dat de tweede naamgeving binnen één jaar na de eerste plaats vindt. Daarna neemt de kans exponentieel af met het verstrijken van de jaren. Wat opvalt is dat de kans hoger begint en sneller daalt dan voor de tweemalige namen. De tweede naam komt in dit geval eerder. Blijkbaar doet het er wel degelijk toe hoeveel kinderen later de naam nog zullen krijgen. Een nieuwe naam heeft blijkbaar een potentie om aan te slaan. Als die potentie er niet is dan blijft het een unieke naam.  Met een beetje potentie krijgt een ander kind de naam ook (figuur 1), maar daar blijft het bij (afgezien van vernoeming), en de tweede naamgeving kan ook gemakkelijk tientallen jaren op zich laten wachten.  Met meer potentie komt een volgende naamgeving sneller. Volgens figuur 2 krijgt voor de helft van de nieuwe voornamen het tweede kind de naam binnen 12,8 jaar. En er zijn modenamen waarbij het proces nog sneller gaat, dat gaan we nog bekijken.

De kans op een verschil in jaren tussen de tweede en de eerste naamgeving laat zich goed met een exponentiële relatie benaderen:  p_1,2(j) = v * (1-v) ^j-1 . Hierin is p_1,2(j) de kans op een verschil in jaren (j) tussen de eerste en de tweede naamgeving. De variabele v kan geïnterpreteerd worden als de verspreidingsfactor, een maat voor de verspreidingssnelheid van de naam, die kan variëren tussen 0 en 1. Als v=0 dan verspreidt een naam zich niet en blijft uniek. Als v naar 1 nadert, dan verspreidt de naam zich heel snel. In dit geval is v = 0,075. Dat is sneller dan voor tweemalige namen werd gevonden (v = 0,03). Wat ik hierboven potentie noemde kun je vertalen als een grotere verspreidings- of imitatiesnelheid.

Een afname van de kans op een tijd tussen twee naamgevingen is ook mogelijk wanneer het totaal aantal voornamen waaruit gekozen kan worden jaarlijks toeneemt, en er aangenomen wordt dat ouders daaruit willekeurig een naam kiezen. Dat is een optie in genetische modellen. Maar daarvoor zouden er elk jaar 8% nieuwe namen moeten worden bedacht. In aflevering 6 zagen we tot 1960 jaarlijks maar 0,5% nieuwe namen. En ook al is dat percentage de laatste jaren door migratie tot 4% gestegen, het geeft een onvoldoende verklaring.

Hoe kende het  tweede ouderpaar de nieuwe naam? Ze hoefden het eerste ouderpaar niet persoonlijk te kennen, maar moeten wel gehoord hebben van de naam. Dat zou gemakkelijker kunnen zijn als ze bij elkaar in de buurt wonen, dan kan de verspreiding van een naam sneller gaan. Wat kan leiden tot de hypothese dat  er een relatie is tussen de tijdsduur tussen de naamgevingen en de afstand tussen de geboorteplaatsen: een korte tijdsduur bij een kleine afstand, een lange tijdsduur bij een grote afstand.  Dat is, met dank aan David Onland, onderzocht en die correlatie is er helemaal niet. De twee geboortegemeenten lagen, ongeacht de tijdsduur tussen de geboorten, gemiddeld 73 km uit elkaar.

Als laatste zou nog gedacht kunnen worden dat er een externe reden is dat ouders op hetzelfde idee komen. Dat zou bijvoorbeeld een naam van een beroemde acteur of zanger kunnen zijn die zich snel via de media verspreidt. Britney Spears is daar in 1999 een goed voorbeeld van. Maar dat gebeurt als (bijna) nieuwe naam in Nederland zelden, en lijkt voor de periode 1920-1960 geen algemene verklaring te bieden.