Voornamendrift (5)

door Gerrit Bloothooft

We geven nu heel andere voornamen aan kinderen dan vroeger. De traditionele vernoemingsnamen zijn van meer dan 75% naar minder dan 5% teruggevallen, en daar zijn in de loop van de 20^e eeuw modenamen voor in de plaats gekomen. Voor de voornamen van de hele bevolking geldt een Zipfiaanse relatie, die het aantal namen met een bepaalde frequentie voorspelt. Maar is die relatie gelijk voor traditionele namen en modenamen?

Om dat te onderzoeken heb ik de voornamen die ons uit de GBA bekend zijn verdeeld in geboorte-intervallen van 10 jaar. Per decade werden tussen 0.8 en 1.0 miljoen jongens en eenzelfde aantal meisjes geboren. Vanaf 1905 zijn ons daarvan voldoende voornamen bekend om de Zipfiaanse relatie n(f) = n(1)/f ^α  te berekenen. Als voorbeeld staan in
figuur 1 zowel de resultaten voor 1905-1914, waar een traditionele vernoemingstraditie overheerst, als voor een eeuw later, 2005-2014, wanneer de modenamen dominant zijn.

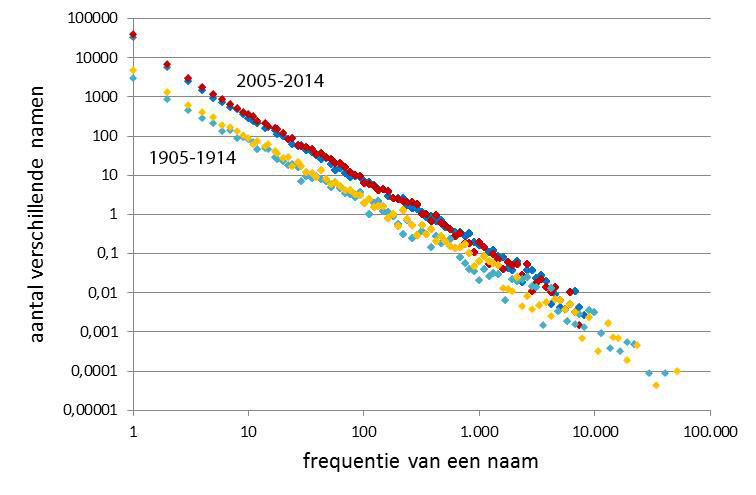
Voor beide decaden liggen de resultaten op een rechte lijn die wat uitwaaiert voor namen met meer dan 1000 naamdragers. Omdat het aantal personen per decade niet gelijk is in onze gegevens, 1905-1914 1.1 miljoen en 2005-2014 1.7 miljoen, liggen de gegevens per decade wat uit elkaar. Alhoewel Zipf geldt voor beide decaden (en voor mannen- en vrouwennamen), verschilt de richting van de lijn iets. Dat komt door de verdeling van de namen. Voor de traditionele namen (1905-1914) zijn er minder unieke namen en halen de populairste namen (Johannes en Maria) veel hogere  frequenties dan topnamen een eeuw later. De richting van de lijn is gegeven door de exponent α waarvan de waarde in figuur 2 per decade uitstaat. Omdat de Zipfiaanse relatie iets afwijkt voor lage en hoge naamfrequenties is de berekening van α alleen over de frequenties 5-1000 uitgevoerd.

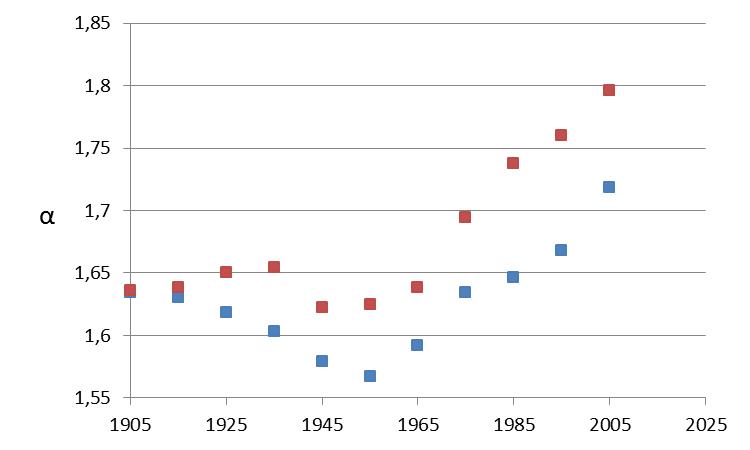
Voor de decaden van 1905-1914 tot 1945-1954 is de waarde van α min of meer constant en voor mannen zelfs wat dalend, maar daarna stijgt α voortdurend. Dat komt overeen met traditionele namen die tot 1950 dominant en zeer stabiel waren, en de opkomst van modenamen en een verbreding van de namenvoorraad door migratie daarna. Tot 1950 werd de topnaam Maria jaarlijks aan 10% van alle meisjes gegeven en Johannes aan 8% van alle jongens.  In 2014 waren de percentages voor topnamen met een factor 10 gezakt: toen werd 0,8% van de meisjes Sophie genoemd en 0,9% van de jongens Daan. Dat is een enorme verschuiving in de verdeling van de namen. Maar voor de Zipfiaanse relatie, die veel meer bepaald wordt door de lage frequenties, is het maar een kleine verandering die op het oog in figuur 1 nauwelijks zichtbaar is. Dat vrouwennamen een algemeen hogere waarde voor α hebben betekent dat ze meer variëren dan mannennamen, wat onder andere blijkt uit meer unieke namen voor vrouwen. De variatie in α die we in figuur 2 zien is zo beperkt dat die voor de hele bevolking niet tot vervorming van de relatie leidt. De Zipfiaanse relatie lijkt in steen gebeiteld, wat duidt op een onderliggend proces dat blijft gelden terwijl de naamgeving totaal verandert. Naar dat proces achter voornaamkeuze gaan we verder op zoek door naar nieuwe namen te kijken: welke blijven uniek en welke worden populair.