Een vrij waarschijnlijk universeel kenmerk van talen is dat ze woorden hebben: de stroom geluiden die uit iemands mond komt, kan worden opgehakt in kleinere stukjes die een vrij duidelijke betekenis hebben en met die betekenis vaker voorkomen in andere stromen geluiden. De grootte van woorden kan verschillen – in onze taal zijn heel veel woorden eenlettergrepig, behalve … [Lees meer...] overWoorden zijn cultuur
Zipf
Een wonderbaarlijke voorspelbaarheid
Voornamendrift 105 We hebben een naam om gekend te worden. Die naam moet ons onderscheiden van de ander. Daarom hebben we niet allemaal dezelfde voornaam. Maar als iedereen een eigen unieke naam zou hebben is dat ook niet werkbaar. Dat zijn precies de twee uitersten waartussen het aantal verschillende voornamen dat we hebben zal liggen: allemaal dezelfde voornaam, of … [Lees meer...] overEen wonderbaarlijke voorspelbaarheid
Opgeteld en voorspeld
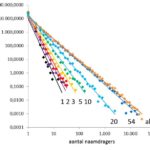
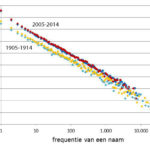
Voornamendrift 104 Er zijn verschillende manieren om de machtswet van voornamen te laten zien, maar die hierboven lijkt me grafisch de mooiste. Voor vier landen/gewest (Vlaanderen, Nederland, Frankrijk, USA) die spreiden in het aantal jaarlijkse geboortes van 40.000 tot 2 miljoen, en voor vijf jaren die een eeuw omspannen. In elke figuur wordt voor jongens cumulatief (het … [Lees meer...] overOpgeteld en voorspeld
Natuurlijke selectie
Voornamendrift 103 Er is iets vreemds met unieke voornamen, het zijn er teveel. Althans, het zijn er meer dan je zou verwachten als je uitgaat van de machtswet van de voornamen. Die (Zipfiaanse) wet voorspelt hoeveel verschillende voornamen n(f) er zijn met een bepaalde frequentie f: n(f) = n(1)* f α. Hierin is n(1) het aantal namen dat precies één keer is gegeven, de … [Lees meer...] overNatuurlijke selectie
Afasie en de vorm van het menselijk geheugen
Door Marc van Oostendorp Sommige dingen hebben alle talen met elkaar gemeen terwijl eigenlijk niemand weet waarom. Het geldt onder andere voor de Wet van Zipf. Zodra je een verzameling taalmateriaal neemt van voldoende omvang, gaat dit aan deze statistische wet voldoen. Gerrit Bloothooft schreef bijvoorbeeld eerder dit jaar uitgebreid over het feit dat hij ook geldt … [Lees meer...] overAfasie en de vorm van het menselijk geheugen
Aan elkaar knopen
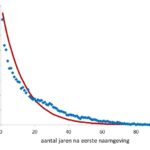
Voornamendrift (27) Door Gerrit Bloothooft Nieuwe voornamen, ze beginnen allemaal met de eerste naamgeving. Een flink aantal blijft een eenmalige vondst van de ouders, andere worden nagevolgd, en een enkele naam wordt heel populair. Die aantallen liggen wonderlijk genoeg vast, in een Zipfiaanse verdeling. Een van de mooiste resultaten die ik in deze serie kon laten zien is … [Lees meer...] overAan elkaar knopen
Nadoen
Voornamendrift (18) Door Gerrit Bloothooft We leren en leven door na te doen en zijn zelden origineel. Dat is misschien wel zo rustig want stel je voor dat we allemaal een unieke voornaam zouden hebben. Hoe we nadoen en kopiëren is trouwens boeiend genoeg. Het is de sleutel om te begrijpen hoe vernieuwingen breed navolging kunnen vinden, of juist niet. De kern van mijn eerdere … [Lees meer...] overNadoen
De ontwikkeling van een Zipfiaanse verdeling
Voornamendrift (16) Door Gerrit Bloothooft Figuur 1. Ontwikkeling van de Zipfiaanse verdeling voor 29.756 nieuwe voornamen uit de periode 1920-1960, voor 1, 2, 3, 5, 10, 20 en 54 jaar na introductie van een naam. Met ook het totale resultaat per 2014. Ik moet bekennen dat ik na 15 afleveringen Voornamendrift nog geen verklaring voor de Zipfiaanse verdeling van voornamen … [Lees meer...] overDe ontwikkeling van een Zipfiaanse verdeling
De voorspellende waarde van het eerste jaar van een nieuwe voornaam
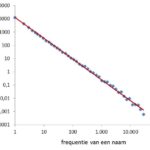
Voornamendrift (15) Door Gerrit Bloothooft Figuur 1. Zipf verdeling van 29.756 voornamen die voor het eerst tussen 1920 en 1960 zijn gegeven, berekend op basis van het gemiddeld aantal namen per logaritmisch interval. In aflevering 11 liet ik zien dat de snelheid van opvolgende naamgevingen na de introductie van een nieuwe naam afhangt van de latere populariteit. Maar … [Lees meer...] overDe voorspellende waarde van het eerste jaar van een nieuwe voornaam
Traditionele namen, modenamen en Zipf
Voornamendrift (5) door Gerrit Bloothooft We geven nu heel andere voornamen aan kinderen dan vroeger. De traditionele vernoemingsnamen zijn van meer dan 75% naar minder dan 5% teruggevallen, en daar zijn in de loop van de 20e eeuw modenamen voor in de plaats gekomen. Voor de voornamen van de hele bevolking geldt een Zipfiaanse relatie, die het aantal namen met een bepaalde … [Lees meer...] overTraditionele namen, modenamen en Zipf
Zipf plus Zipf blijft Zipf
Voornamendrift (4) Door Gerrit Bloothooft Onze voornamen zijn een mengelmoes. Er zijn traditionele voornamen van christelijke of germaanse oorsprong, er wordt geleend van omringende talen in Europa, en door migratie kunnen we voornamen uit de hele wereld tegenkomen. En toch vinden we alles bij elkaar voor de hele bevolking een aantal voornamen met een bepaalde frequentie dat … [Lees meer...] overZipf plus Zipf blijft Zipf
Oplossing voor taalkundig probleem van 100 jaar oud
(Persbericht Radboud Universiteit) Wist je dat in iedere taal het meest voorkomende woord ongeveer twee keer zo vaak voorkomt als het op een na meest voorkomende woord? Deze wet genaamd ‘Zipf’s law’ is al ruim een eeuw oud, maar tot nu toe lukte het wetenschappers niet om het verschijnsel precies te verklaren. Taalwetenschapper Sander Lestrade van de Radboud Universiteit … [Lees meer...] overOplossing voor taalkundig probleem van 100 jaar oud