'Category Theory for Neuroscience (pure math to combat scientific stagnation)' – zo'n titel werkt voor mij als click bait. Pure wiskunde! Categorietheorie! Neurowetenschap! Wetenschappelijke stagnatie bestrijden! De spreker is Alexander Maier, een Amerikaanse psycholoog – zo te zien niet de allergrootste ster op het gebied, maar ook geen kleine jongen. Toch is het een wat … [Lees meer...] overCategorietheorie en structuralisme
wiskunde
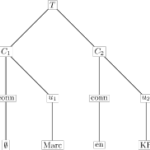
De wiskundige structuur van de zin ontrafeld
94 jaar oud is Noam Chomsky nu, en vorige maand verscheen een klein nieuw hoogtepunt in zijn oeuvre, een artikel dat weer een aantal dingen op zijn kop zet, en misschien een nieuwe richting wijst in de studie van de zinsbouw. Ja, Chomsky is van dit artikel 'maar' de tweede auteur, en het is heel waarschijnlijk dat het artikel voor een groot deel uit de koker komt van de eerste, … [Lees meer...] overDe wiskundige structuur van de zin ontrafeld
When Linguists do Set Theory
Presentation by K.P. Hart (Delft University) … [Lees meer...] overWhen Linguists do Set Theory
Taalkunde in het wiskunde-examen
Vanmiddag vindt het centraal examen Nederlands voor vwo plaats, en we weten allemaal wat de kans is dat daarin een taalkundig artikel aan bod komt: 1 – 0.9999... Gelukkig was er eerder deze week al het eindexamen Wiskunde A, want daarin ging het wél over taal. Althans, één van de vragen verwees naar een onderzoek uit 2013 over het gebruik van ronde getallen door links- en … [Lees meer...] overTaalkunde in het wiskunde-examen
10 oktober 2020, online: Symposium ‘In de geest van Stevin’
26e symposium van de NVvW werkgroep Geschiedenis Met dit thema vragen we aandacht voor de rijke nalatenschap van Simon Stevin, die 400 jaar geleden overleed. Stevin hield zich met veel verschillende onderwerpen bezig, zowel theoretisch als in de praktijk: technologie, wiskunde, mechanica, boekhouden, economie, onderwijs, taal, oorlogsvoering, perspectief in afbeeldingen, … [Lees meer...] over10 oktober 2020, online: Symposium ‘In de geest van Stevin’
Trek meertaligheid ook door naar je evaluatiepraktijk
Door Steven Delarue Telkens als ik een doctoraatsverdediging bijwoon, denk ik onvermijdelijk terug aan die van mij, intussen bijna een jaar of vier geleden. Het is een dag die ik toen grotendeels in een roes heb beleefd, door alle stress, emotie en adrenaline die ermee gepaard ging, en waarvan ik me vooral het verlossende applaus herinner dat volgde op de melding van de … [Lees meer...] overTrek meertaligheid ook door naar je evaluatiepraktijk
Sommen maken is vertalen
In sommige opzichten is de wereld een beetje beter geworden tijdens de quarantaine: in je eigen woonkamer kun je nog gemakkelijker dan voorheen geleerde betogen over allerlei onderwerpen bijwonen die op het eerste gezicht misschien ver van ons neerlandistische bed zijn, maar daar toch aardig in passen. Neem de bovenstaande lezing, gisteren online geplaatst als deel van het … [Lees meer...] overSommen maken is vertalen
Zijn natuurlijke talen groter dan verzamelingen?
Door K.P. Hart Dit is de vierde in een korte serie blogposts naar aanleiding van een discussie op twitter over dit stuk op Neerlandistiek van Marc van Oostendorp dat zelf weer een reactie op dit artikel van Paul Postal was. In de eerste post kwalificeerde ik een opmerking uit het stuk van Postal als lariekoek. Daar gaat deze post over. … [Lees meer...] overZijn natuurlijke talen groter dan verzamelingen?
Boekenplanken voor gevorderden
Door K.P. Hart In dit vervolg op deze blogpost ga ik het hebben over het ordenen van boeken. Bij de twitterdiscussie over er verschil is, of niet, tussen boeken en getallen kwam ook de mogelijkheid getallen en boeken te ordenen ter sprake. Hierbij werd met `getal’ stilzwijgend `natuurlijk getal’ bedoeld. Nu komen natuurlijke getallen met een natuurlijke ordening, waarin … [Lees meer...] overBoekenplanken voor gevorderden
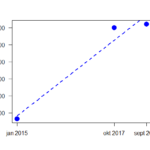
De factchecker gefactcheckt: exponentiële groei
Door Freek Van de Velde Bart De Wever, de populairste rechtse politicus in Vlaanderen, heeft een boek geschreven over ‘identiteit’. Daarin schrijft hij “Het aantal begunstigden van een leefloon is sinds 2015 exponentieel gestegen tot meer dan 140.000 in 2017.” Die uitspraak is onder de loep genomen in de ‘factcheck’-rubriek van de krant De Standaard van 8 mei. Taalkundig … [Lees meer...] overDe factchecker gefactcheckt: exponentiële groei
Schoonheid is begrijpelijkheid
Door Marc van Oostendorp Een curieus verschijnsel is dat wetenschappers hun grote ideeën eigenlijk alleen nog uitdrukken in boeken voor een breder publiek. Hoe zit het universum precies in elkaar? Wat zijn de grenzen aan de wetenschap? Nooit schrijft iemand een wetenschappelijk artikel over die vragen, terwijl het artikel eigenlijk de enige vorm is waarin je in veel … [Lees meer...] overSchoonheid is begrijpelijkheid
Wie is er bang voor de neerlandistiek?
Door Marc van Oostendorp Weinig schoolvakken hebben zoveel pleitbezorgers in het publieke leven als de wiskunde. Het kan aan mijn beperkte blik liggen, maar ik hoor zelden iets wervends van pakweg een Nederlandse chemicus of aardrijkskundige, terwijl de boeken van wiskundigen als het ware niet aan te slepen zijn en ik als volstrekte leek zo al gemakkelijk vijf Nederlandse … [Lees meer...] overWie is er bang voor de neerlandistiek?
13 januari 2018, Utrecht: Wintersymposium 2018 Wiskunde en Taal
zaterdag, 13 januari 2018, 11.00 – 16.00 Aula van het Academiegebouw van de Universiteit Utrecht (Domplein) Wiskunde en taalkunde kennen fascinerende raakvlakken. De wiskunde kan ons iets leren over taaluitingen, aan beide liggen logische denkpatronen ten grondslag – en natuurlijk wordt wiskunde zelf ook gezien als taal! Dat uit zich ook in de schoolprogramma’s: van … [Lees meer...] over13 januari 2018, Utrecht: Wintersymposium 2018 Wiskunde en Taal
2000 twijfelachtige stukjes
Door Marc van Oostendorp Omdat ik deze week mijn 2000e stukje op Neerlandistiek heb geplaatst, heb ik eens door wat oudere blogs gebladerd. Sommige was ik vergeten en die zijn natuurlijk altijd het leukst, want mijn posts gaan onveranderlijk over onderwerpen die mij interesseren. Ik schreef precies vijf jaar geleden bijvoorbeeld over de vraag hoe reëel een kans is … [Lees meer...] over2000 twijfelachtige stukjes
De wiskunde van erbij horen
Door Marc van Oostendorp Het gebruik van wiskundige modellen verdeelt de taalwetenschappelijke gemeenschap in drieën. Er is een groep die iedere vorm van wiskunde volkomen wantrouwt en vindt dat het verkeerd is om de vloeibare sociale en psychologische werkelijkheid van de taal op wat voor manier dan ook in formules te vangen; naar mijn indruk zitten in deze groep momenteel … [Lees meer...] overDe wiskunde van erbij horen
Hoe kunnen we over getallen spreken?
Door Marc van OostendorpIn mijn zondagmiddagminicollege leg ik uit waarom taal volgens de Amerikaanse psychologe Elisabeth Spelke cruciaal is bij het ontstaan van getallen. … [Lees meer...] overHoe kunnen we over getallen spreken?
De prijs die wij mensen voor taal betaald hebben: een slechter geheugen
Taal en getal (3)Door Marc van OostendorpIllustratie: M. van OostendorpDe vraag in hoeverre mensapen taal hebben, of kunnen leren, of in ieder geval rudimenten hebben van menselijke taal heeft de mensheid lang gefascineerd, en terecht. Het is evolutionair gezien heel wonderlijk dat wij zoiets zo ingewikkelds bezitten – daar moeten onze naaste verwanten toch op zijn minst al … [Lees meer...] overDe prijs die wij mensen voor taal betaald hebben: een slechter geheugen
Wiskunde en taal zijn verschillend
Taal en getal (2)Door Marc van Oostendorpillustratie: M. van OostendorpWiskundigen gebruiken een heel ander deel van hun hersenen om over wiskundige problemen na te denken dan om naar taal te luisteren. Wanneer je ze mondeling een probleem geeft, zie je eerst even de taalcentra werken, maar daarna speelt de activiteit zich af in een heel ander hersengebied – dat van de … [Lees meer...] overWiskunde en taal zijn verschillend
Wie heeft er meer tandpasta?
Taal en getal (1) Om een taal goed te spreken, moet je een beetje kunnen tellen. Vaak lijkt dat tellen nogal simpel: voor het Nederlands volstaat het op het eerste gezicht vaak om het verschil te begrijpen tussen één en meer dan één, tussen enkel- en meervoud. Wie wil beweren dat hij Nederlands spreekt, zal het verschil moeten begrijpen tussen 'een hond wandelt' en 'honden … [Lees meer...] overWie heeft er meer tandpasta?
Hoe lang duurt het pellen van een mandarijn?
Door Marc van OostendorpIk ken weinig dichtbundels waarin de liefde voor het grote getal zo uitbundig wordt gevierd als het deze week met de Herman de Coninck-prijs bekroonde Lichtmeters van Ruth Lasters. Waarom hebben dichters dat niet eerder ontdekt, denk je dan – de wonderlijke poëzie van het heel, heel grote, van de vele lichtjaren.Dat geldt bijvoorbeeld voor … [Lees meer...] overHoe lang duurt het pellen van een mandarijn?
Is het Nederlands triviaal?
Door Marc van Oostendorp De Britse wiskundige Alex Bellos schreef gisteren in The Guardian een artikel dat ook in Nederland enig stof deed opwaaien. In dat stuk besprak Bellos het feit dat de Engelse spelling triviaal is: als je ieder woord ziet als een vermenigvuldiging, en iedere letter als een variabele in die vermenigvuldiging, dan kun je bewijzen dat … [Lees meer...] overIs het Nederlands triviaal?
Bestaat er iets voor taal wat vergelijkbaar is met het getal nul voor de wiskunde en exacte wetenschap?
Onverwachte taalvragen aan de Nationale Wetenschapsagenda (9)Door Marc van OostendorpSommige onderzoekers wezen er in de aanloop naar de Nationale Wetenschapsagenda op dat de initiatiefnemers van die agenda uitgingen van een verkeerd idee: dat onderzoekers er zijn om vragen te beantwoorden. Een belangrijk deel van hun werk bestaat er juist uit om de goede vragen te … [Lees meer...] overBestaat er iets voor taal wat vergelijkbaar is met het getal nul voor de wiskunde en exacte wetenschap?
Op de allereende plaats?
Door Marc van Oostendorp Er gebeurt zoveel tegelijkertijd dat je soms pas jaren later hoort over dingen die naast de deur gebeurd zijn. Zo kwam ik er gisteren toevallig pas achter wat een interessant artikel mijn collega Sjef Barbiers – hij zit hier op het Meertens Instituut twee deuren verder te typen – in 2007 geschreven heeft: een artikel over één en veel. (U moet er … [Lees meer...] overOp de allereende plaats?
Wil je koffie of thee?
Over taal en wiskunde In een aardige blogpost beschreef de wiskundige Ionica Smeets gisteren de taalopvatting van haar vakgenoten: Ik ken [...] wiskundigen die de vraag ‘Wil je koffie of thee?’ steevast met een triomfantelijk ‘Ja’ beantwoorden. Mijn collega’s hebben een wat merkwaardig gevoel voor humor, en ze gebruiken taal anders dan de meeste mensen. Hun zinnen zijn logisch … [Lees meer...] overWil je koffie of thee?