Door Freek Van de Velde
Bart De Wever, de populairste rechtse politicus in Vlaanderen, heeft een boek geschreven over ‘identiteit’. Daarin schrijft hij “Het aantal begunstigden van een leefloon is sinds 2015 exponentieel gestegen tot meer dan 140.000 in 2017.” Die uitspraak is onder de loep genomen in de ‘factcheck’-rubriek van de krant De Standaard van 8 mei.
Taalkundig boeiend is de passage over de semantiek van ‘exponentieel’. De fact-checkende journalist schrijft: “Maar klopt die inschatting wel? We nemen de officiële cijfers van de overheidsdienst Maatschappelijke Integratie er even bij. Die leren dat er sinds begin 2015 tot september 2018 (laatste cijfers) 32.735 leefloongerechtigden zijn bijgekomen, tot een recordaantal van 144.151. De kaap van de 140.000 werd inderdaad in oktober 2017 overschreden. Wiskundig gezien gaat het hier niet om een exponentiële stijging, maar we vermoeden dat De Wever het figuurlijk heeft over een ‘erg sterke’ stijging. En die was er zeker.”
Het verdict is dus: er is een letterlijke, wiskundige betekenis van het woord ‘exponentieel’ en er is een figuurlijke betekenis van het woord ‘exponentieel’. En, zo legt de journalist ons geduldig, maar een tikkeltje betweterig uit, uiteraard heeft De Wever hier de figuurlijke betekenis op het oog, want de wiskundige betekenis is hier uitgesloten.
Maar laat ons die uitspraak eens fact-checken (in het volle besef dat dit nóg betweteriger is).
Exponentiële curves
Er zijn tussen 2015 en 2018 32.735 leefloners bijgekomen tot 144.151. Kan die stijging op drie jaar wiskundig gezien een exponentiële groei zijn? Natuurlijk wel. Door twee punten kun je een rechte trekken (lineaire groei), of een polynomiaal, maar net zo goed een exponentiële curve. Die heeft, in eenvoudige gedaante, de vorm f(t)= abt. Als we 1 januari 2015 herijken als 0 op de tijdsas, en 1 september 2018 als 44 (gerekend in maanden dus), dan krijgen we: 144151-32735= ab0 dus a is alvast 111416, en dan: 144151 = 111416*b44, waaruit volgt dat
Dus de vergelijking wordt
Maar er staat meer in de tekst: we lezen dat in oktober 2017 de kaap van de 140.000 al overschreden is. Dat is na 33 maanden. Als we onze vergelijking gebruiken, dan krijgen we:
wat uitkomt op iets meer dan 135.000. De rode curve ‘mist’ het punt in 2017.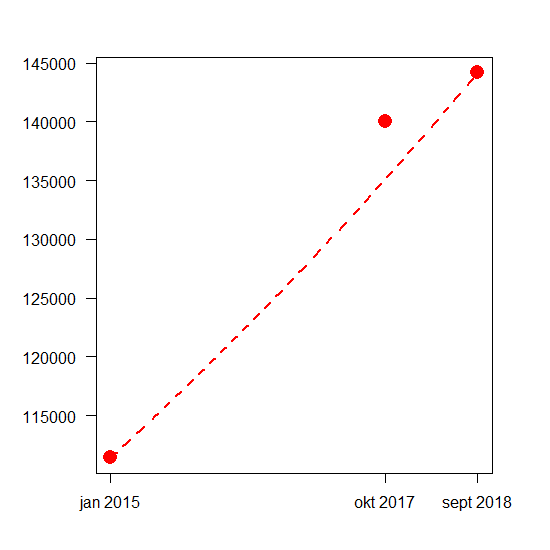 Dus wiskundig toch geen exponentiële curve? Geen nood!
Dus wiskundig toch geen exponentiële curve? Geen nood!
Meer exponentiële curves
Exponentiële functies kunnen complexere vormen aannemen, met nog een as-afsnede en wat gepriegel in de exponent: f(t)= a+bect. Vooral die a kunnen we goed gebruiken om die 140.000 leefloners in oktober 2017 in een exponentieel verhaal te wringen en niemand zegt dat we geen negatieve b en c mogen gebruiken. Negatieve exponenten zijn ook exponenten. Met de exponentiële functie
zitten we exact op de datapunten (blauw).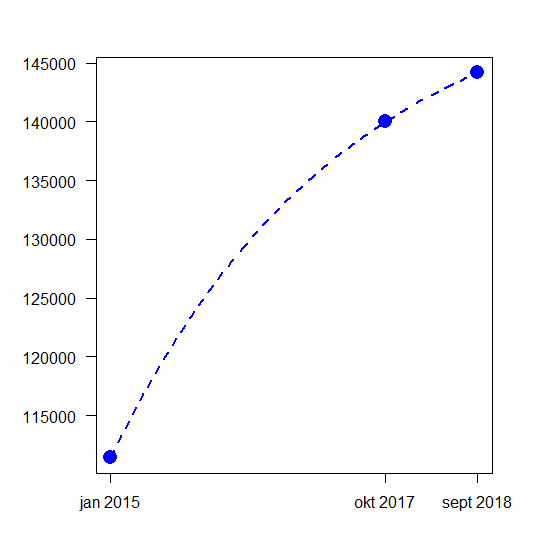
Bovendien verwachten we niet dat de geobserveerde waarden exact op de geïdealiseerde curve liggen. In de realiteit heb je ruis (‘residuelen’), en statistische curves proberen patronen in die ruis te ontwaren, met een tolerantie voor fouten. En sowieso verwachten we nog schommelingen volgens de seizoenen, dus het hoeft niet eens een echte monotoon stijgende curve te worden.
Dus of het echt een exponentiële groei is, is helemaal niet uit te maken met twee waarden op twee verschillende tijdstippen, en zelfs met drie waarden op drie verschillende tijdstippen is het een hachelijke zaak precieze onderliggende curve te beoordelen. Je hebt exponentiële curves die met het blote oog niet van lineaire trajecten te onderscheiden zijn.
Wiskunde, intuïtief benaderd
Hoe moeten we nu weten of het met die leefloners gaat om een exponentiële curve? Daarvoor zou je kunnen nadenken over de aard van exponentiële groei. ‘Exponentieel’ is eigenlijk de wiskundige vertaling van een intuïtief idee: dat de groei van de populatie door de tijd heen evenredig is met de populatie. Anders gezegd: dat de toename van aantal leefloners in de tijd groter is naarmate er meer leefloners zijn. Dat wordt weergegeven in een simpele differentiaalvergelijking: d(leefloners)/dt = groeifactor * leefloners.
Nu kun je je afvragen: is het überhaupt plausibel dat de toename van het aantal immigranten met een leefloon groter wordt naarmate er meer immigranten zijn met een leefloon. Dat is in principe niet onmogelijk. Je kunt je een scenario voorstellen waarin die immigranten naar huis bellen en zeggen: ‘je moet naar België komen, daar krijg je een leefloon’, waarop die mensen ook weer bellen naar hun neefjes en nichtjes enzovoort. De Wevers partijgenoot Theo Francken noemt dat het ‘aanzuigeffect’.
Meestal stuit dat soort groei op draagkrachtbeperkingen: na een tijdje is het aantal leeflonen dat uitgekeerd kan worden op. Dat heet ook wel: de Tragedie van Malthus. Wat je dan ziet is dat de toename van het aantal leefloners in de tijd evenredig is met het aantal leefloners, maar óók evenredig met een factor 1 – leefloners/draagkracht. Dus: d(leefloners)/dt = groeifactor * leefloners * (1 – leefloners / draagkracht). Die extra factor zorgt ervoor dat de exponentiële curve afneemt wanneer je de draagkracht nadert. Je krijgt dan een s-curve, met een steil stijgend middenstuk. Die curve heet de ‘logistische functie’, en is ontdekt door een Belg, Pierre François Verhulst, in de 19e eeuw. Misschien had De Wever, in een vlaag van Vlaams chauvinisme, trots kunnen zijn op de Vlaamse universiteit waar Verhulst later lesgaf (Gent), en had hij beter gezegd: “als het aanzuigeffect klopt, en we hebben geen eindeloos groeiende enveloppe voor de uitkering van leeflonen, dan kunnen we vermoeden dat we het aantal leefloners in een logistische curve zien stijgen”. Want ‘exponentieel’ is te ambigu.
(Dit stuk is een wijziging van een eerder stuk, waarin nog een fout stond – Dank aan Stefano De Pascale voor de opmerkzaamheid!)
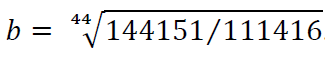
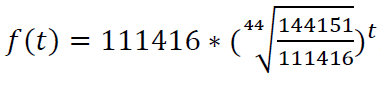
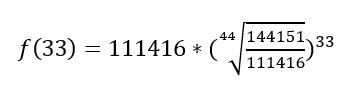
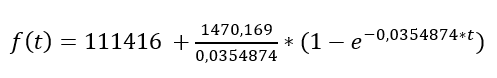
Flashback naar een tweedekan-seminarieachtig iets dat u vijftien jaar geleden gaf waarbij we een tekst moesten schrijven om een paar grafieken te verklaren. Dat stelde ook hoge eisen (positief bedoeld).
Ja, mijn allereerste jaren aan de faculteit. We hebben het allebei overleefd.