Voornamendrift (15)

Door Gerrit Bloothooft

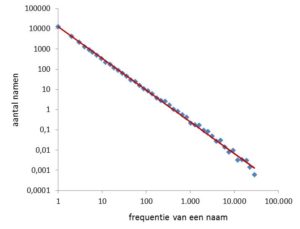
In aflevering 11 liet ik zien dat de snelheid van opvolgende naamgevingen na de introductie van een nieuwe naam afhangt van de latere populariteit. Maar alhoewel het daar een voorbode van is, merkte Daan Wesselink in een reactie terecht op dat de voorspellende waarde ook afhangt van het aantal namen dat uiteindelijk een bepaald aantal naamdragers krijgt. Als dat Zipfiaans verdeeld is, dan mogen snelle volgende naamgevingen weliswaar zeldzaam zijn voor laag frequente namen, maar omdat er van de laatsten zo veel zijn, zou het toch gemakkelijk een niet-populaire naam kunnen betreffen. Hij heeft gelijk en ik werk dat hier verder uit. Eerst moet onderzocht worden of voor de 29.756 nieuwe voornamen uit de periode 1920-1960 de Zipfiaanse relatie geldt. En ja, dat is zo (figuur 1).

Om een indruk te krijgen over welke namen we het eigenlijk hebben staan hieronder de top-10 voor jongens en voor meisjes, met het jaar van introductie, het topjaar of topjaren als er twee duidelijke pieken te onderscheiden zijn, en het totaal aantal naamgevingen tot en met 2014. De namen doen er 40 tot 80 jaar over om in de laatste decennia van de vorige eeuw de top te bereiken, en er zijn opvallend veel namen bij die twee toppen hebben, zoals eerder bij Femke besproken. Er zijn ook veel Engelse namen bij die erg populair waren in de jaren 90, maar hun start al voor 1950 hadden.

top-10 jongens

naam                   1e jaar  topjaar                aantal
Tim                         1924       2000                      31.005
Kevin                      1948       1992                       23.926
Robin                     1920       1976,1992              23.617
Roy                         1925       1989                        20.687
Rick                        1949       1991,1999              19.236
Mike                       1928       1974,1993              17.841
Danny                    1945       1974,1984              17.481
Remco                   1927        1975                        17.167
Jeffrey                   1949        1970,1991              15.975
Luuk                      1925        2011                        14.661

top 10 meisjes
naam                   1e jaar  topjaar               aantal
Sandra                   1924       1971                       28.867
Kim                        1936       1980,1997             26.269
Karin                      1921       1969,1981             24.268
Chantal                  1937       1974,1987             20.591
Wendy                   1941        1974                      20.200
Patricia                  1921        1971,1978             19.997
Anouk                    1945       1976,1998             19.633
Nicole                    1925        1969,1987            19.025
Miranda                1935        1972                      17.291
Joyce                     1923        1986                      16.300

Ik onderzoek nu of het aantal kinderen dat in het jaar van introductie een naam krijgt een voorbode is voor latere populariteit. De kans daarop is gelijk aan de kans op een aantal naamdragers in het eerste jaar (die afhankelijk is van de uiteindelijke frequentie) maal de kans op een naam met die frequentie (volgens Zipf, figuur 1).

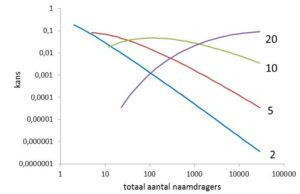
Figuur 2 geeft het resultaat wanneer respectievelijk 2, 5, 10 of 20 kinderen in het introductiejaar de naam krijgen. Wanneer 2 kinderen de naam in het eerste jaar krijgen ligt, zoals Daan Wesselink veronderstelde, de top van de verdeling bij laagfrequente namen omdat er daar (zie de Zipf-verdeling in figuur 1) zoveel van zijn. Maar als het aantal kinderen in het eerste jaar toeneemt verschuift de top van de verdeling naar een steeds hoger aantal uiteindelijke naamdragers. Dat is niet verwonderlijk, maar een startende naam die meteen 20 naamdragers krijgt is ook wel weer heel uitzonderlijk (of er iets bijzonders aan de hand, zoals met Britney). Doorgaans zal een nieuwe naam in de beginjaren nog niet veel prijs geven van later succes.

• Figuur 1: Zipf verdeling voor 29.756 voornamen (jongens en meisjes) die in de periode 1920-1960 voor het eerst zijn gegeven: n(f) = 12.672 * f ^-1,57. De exponent -1,57 stemt overeen met in aflevering 5 gegeven waarden.
• Figuur 2: De kans op k naamdragers in j jaar vereenvoudigt voor het eerste jaar tot een evenredigheid met v^k-1 (vergelijk bv p_1,3(j)= v² * (1-v) ^j-1 * j wat voor j=1 gelijk wordt aan p_1,3(1) = v²). v kan uitgedrukt worden in het uiteindelijk aantal naamdragers f op basis van modellering van P_1,2(j), P_1,3(j), P_1,4-10(j), P_1,11-100(j), P_1,101-500(j), en geschat worden als v = 0,02 *(ln(f) + 1). De kans op een totaal aantal naamdragers als k namen binnen een jaar gegeven worden is dan (volgens Bayes) evenredig met
  p(P(_1,k(1)|f) * n(f) ofwel v^k-1 * n(f) = (0,02 *(ln(f) + 1))^k-1* 12.672 * f ^-1,57.