Voornamendrift (3)
Door Gerrit Bloothooft
Er zijn populaire voornamen en er zijn zeldzame en unieke voornamen, en alles daar tussenin. Met een voornaam bedoel ik hier de eerste, officiële voornaam, en niet de roepnaam want die wordt in de bevolkingsadministratie niet geregistreerd. Voor elke voornaam weten we het aantal naamdragers en we kunnen bijvoorbeeld tellen hoeveel namen uniek zijn, want door één persoon gedragen. Zo kunnen we ook het aantal namen tellen waarvoor er precies twee naamdragers zijn, enzovoort. Dat kunnen we doen tot de hoogste aantallen naamdragers, voor welk aantal er dan meestal maar één, populaire naam is. Er blijkt nu een opmerkelijk verband te zijn tussen het aantal verschillende voornamen en het aantal naamdragers ervan. Deze relatie is sterk verwant aan de bekende wet van Zipf.
De relatie kan worden beschreven als: het aantal namen met frequentie f, n(f) = constante/f α . Omdat het aantal namen exponentieel met de frequentie afneemt, noemen we dit ook wel een machtsrelatie (of power law). Deze formule is iets anders dan die welke Zipf gebruikt om de frequenties van woorden, geordend van meest naar minst frequent, te beschrijven. Ook al gaat het om hetzelfde fenomeen, ik vind het gebruik van rangorde minder inzichtelijk. Toch zal ik de relatie Zipfiaans noemen. Door frequentie =1 in te vullen vinden we direct dat de constante gelijk is aan het aantal unieke namen, n(1). Voor een mooie visualisatie nemen we links en rechts de logaritme en krijgen log(n(f)) = log(n(1)) – α log(f). Wanneer we grafisch zowel het aantal verschillende namen als de frequentie logaritmisch uitzetten dan wordt dat een rechte lijn met richtingscoëfficiënt -α. Zo staat het in figuur 1 voor de Nederlandse mannennamen (gegevens uit 2014).
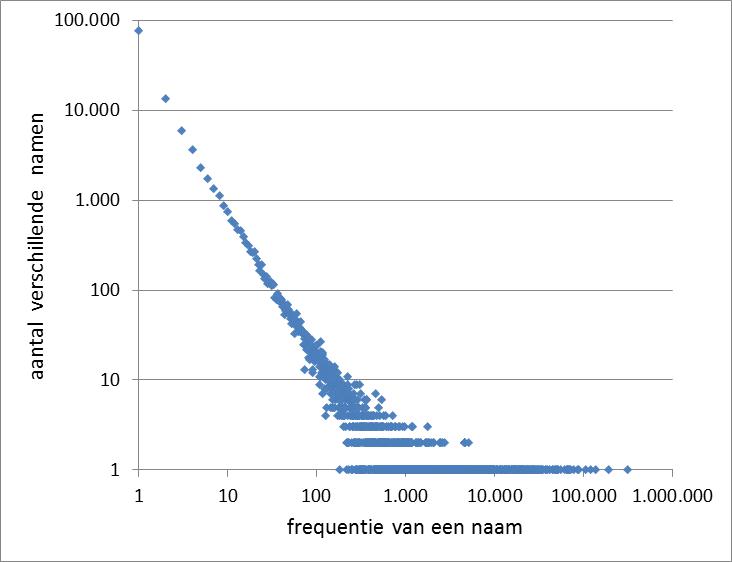
Alhoewel voor lage frequenties de relatie direct voldoet, zien we vanaf de midden frequenties horizontale lijnen omdat er een geheel aantal verschillende namen wordt gevonden, terwijl er daarnaast – en dat is minder goed te zien – bij midden en hogere frequenties veel frequenties zijn die nul scoren, waarbij geen voornaam gevonden wordt. Dat onrustige beeld kan worden voorkomen door het gemiddeld aantal verschillende namen voor een frequentie interval te berekenen. Elk interval krijgt een gelijke breedte op de logaritmische schaal; daarvoor wordt elk volgend interval 10% breder in frequentie gemaakt. Voor lage frequenties maakt dat weinig uit, maar daarna krijgen we tot hoge frequenties een veel duidelijker beeld van de Zipfiaanse relatie (figuur 2). Wel worden de gemiddelden veel kleiner dan 1, omdat de meeste frequenties in het interval dan nul scoren. Door die eenvoud wordt het mogelijk om de relatie voor zowel de vrouwen- als mannennamen te tonen in figuur 2.
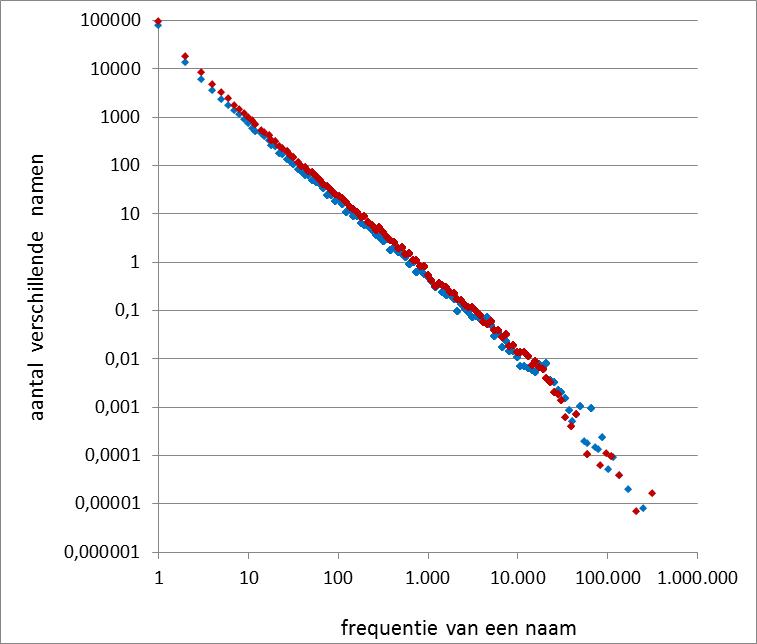
Wat onmiddellijk opvalt is dat de Zipfiaanse relatie fantastisch voldoet. Voor frequenties tussen 5 en 10.000 worden de gegevens benaderd door een rechte lijn met α = 1.63 (vrouwen) en α = 1.60 (mannen). Alleen voor frequenties kleiner dan 5 en groter dan 10.000 is de benadering door een rechte lijn, met minimale spreiding, niet helemaal adequaat. Van de unieke namen (frequentie = 1) zijn er bijna drie keer meer dan voorspeld ( 96.793 unieke vrouwennamen en 77.454 unieke mannennamen), terwijl er van de meest populaire namen minder zijn. Wat ook opvalt is dat de rechte lijn voor zowel mannen- als vrouwennamen voldoet, maar dat er bij de meeste frequenties meer verschillende namen voor vrouwen zijn, wat in overeenstemming is met het grotere totaal aantal verschillende vrouwennamen, 154.250 tegen 120.171 voor mannen. Dat verschil is van alle tijden, vrouwen geven meer aanleiding tot naamvariatie omdat ze vaak door movering van een mannennaam zijn afgeleid, met een keur aan verkleinvormen. Dat verschil geldt niet alleen voor de unieke namen (die 60% van alle verschillende namen omvatten), maar spreidt zich met regelmaat over alle frequenties. Dat is niet vanzelfsprekend en iets om te onthouden.
Om deze abstracte beschrijving meer inhoud te geven, geef ik hieronder voorbeelden van unieke voornamen voor mannen en vrouwen (geboren voor 1917), de namen met een frequentie van 200, en de top-10 voor beiden. Omdat het om de voornamen van de hele bevolking in 2014 gaat, domineren de traditionele namen in de top-10 omdat de tegenwoordige modenamen maar een beperkt aantal jaren gegeven worden en zelfs in topjaren lang niet zo veel, waardoor het totaal aantal naamdragers van top-modenamen vooralsnog zwaar achterblijft bij de traditionele namen van de ouderen.
geboren in 1917 met een unieke naam:
Mannen: Ibelink, Pylger
Vrouwen: Dephine, Duwtje, Elisabetje, Habbediena, Jerijntje, Lauwrijntje, Leenderdina, Leenna, Leijsbetje, Melchertine, Risselmina, Theerske
precies 200 naamdragers:
Mannen: Ahmad, Georges, Jerrel, Koendert, Robbe, Seine, Tijme
Vrouwen: Angelien, Anthonetta, Basma, Katherina, Lissy, Samanta
top-10:
Mannen: Johannes (307.004) , Jan, Cornelis, Hendrik, Willem, Petrus, Pieter, Gerrit, Wilhelmus, Peter
Vrouwen: Maria (334.497), Johanna, Anna, Cornelia, Elisabeth, Wilhelmina, Catharina, Hendrika, Adriana, Petronella
Een theoretisch betere presentatie van de Zipfiaanse relatie is gebaseerd op de cumulatieve verdeling (het totaal aantal verschillende voornamen met een gelijke of hogere frequentie dan f). Die vind ik echter minder inzichtelijk. De hier en later te geven waarden van α zijn echter wel op de cumulatieve verdeling gebaseerd ook al verschillen ze weinig van de waarden die uit de presentatie van gemiddelden zijn afgeleid.
De ‘kloppendheid’ van Zipf komt voort uit het verschijnsel ‘rangorde’ dat wordt gemeten.
Wet van Zipf alhier toegepast verklaart me nog niet meer over het materiaal dan de naamfrequenties zelf.
Ik laat hier inderdaad alleen zien dat er een met Zipf voor tekst vergelijkbare relatie bestaat tussen aantal voornamen met een bepaalde frequentie. Daar zal ik in komende afleveringen dieper op ingaan. Wat een rol speelt is het ontstaan/bedenken van nieuwe namen en of en hoe namen populair worden in de loop van de tijd.
De kern van de wet van Zipf is dat het meeste voorkomende woord komt twee keer zo vaak voor als het op een na meest voorkomende woord, drie keer zo vaak als het woord daarna, en zo door tot aan het minst voorkomende woord. Ik geloof dat dit bij voornamen niet het geval is, maar ik kan de wiskundige achtergronden moeilijk interpreteren.
Vorig jaar verscheen hier op neerlandistiek.nl een oplossing voor de wet van Zipf gevonden door onderzoekers van de Radboud universiteit. Dat was dit persbericht:
https://neerlandistiek.nl/2017/08/oplossing-voor-taalkundig-probleem-van-100-jaar-oud/
Kan iemand hier in een artikel nog eens een en ander goed uitleggen? In mijn beperkte optiek lees ik nog geen verklaring van de wet van Zipf. Ik vind het een uiterst raadselachtig verschijnsel dat mijn ratio te boven gaat. Of denk ik niet wiskundig genoeg?
(En ik had aan Gerard Bloothoofd al eens een de vraag gesteld wat de meest voorkomende voornaamlettercombinaties zijn, ik dacht dus M, MA en MAR. Misschien dat ik er nog eens een antwoord op kriijg in een van de vervoilgartikelen.)
Ik had dat artikel van Sander Lestrade et.al. ook willen aanhalen. Het punt daar is dat het probeert de *afwijkingen* tov de Zipf-wet te verklaren. Dat kan door middel van equivalentieklassen: woorden onlenen een gedeelte van hun informatiewaarde aan de groep(en) waartoe ze behoren. In dit geval is dat de POS-tag. Iets soortgelijks is eerder al gedaan met domein-specifieke jargonwoorden, die ook een verstoring van de wetmatigheid kunnen verklaren. (the long tail)
In het geval van de telwoorden lijkt me ook een factor dat ze vaak in een *rijtje* geleerd worden: een,twee,drie,vier,… . Dat maakt memoriseren makkelijker, en dus worden ze sneller geleerd. Iets soortgelijks zou ik verwachten bij weekdagen: maandag,dinsdag,woensdag,… en maanden. Of kleuren: rood,oranje,geel,groen…
En: kinderen zijn trots op het kennen van die rijtjes.
[Ojee, voorgaande was dus eigenlijk meer een reactie op dat andere Zipf-topic …]
Zipf ordent woordfrequenties van hoog naar laag en je krijgt inderdaad ongeveer rangorde = constante/frequentie. In het begin van de ordening is er bij een hoge frequentie maar één woord met die frequentie maar bij lagere frequenties kunnen er meer zijn, en er zijn ten slotte heel veel woorden die maar één keer voorkomen. Voor voornamen draai ik het om, en tel het aantal verschillende woorden dat een bepaalde frequentie heeft. Je vindt hetzelfde verschijnsel dan op een iets andere manier.
Voor voornamen is de relatie, anders dan bij woorden, inderdaad niet omgekeerd evenredig. Bij Zipf voor woorden ligt de aandacht op de hoge frequenties (rangorde 1,2 etc). Ik leg vooral de nadruk op de lage frequenties. Niet alleen is de relatie daar ook fraai, maar namen met een lage frequentie (waarvan er wel veel verschillende zijn) tonen ook iets van het ontstaan van vernieuwing. Daarbij speelt het proces van populair worden, dus hoe hoge frequenties bereikt worden, ook een rol. Omdat juist de laatste jaren voornamen een snel vernieuwingsproces doormaken, via de modenamen, en we daar een volledig zicht op hebben, is het interessant om dat in detail te bekijken.
Alhoewel voornamen ook een woordsoort vormen, is de verklaring van een Zipfiaanse relatie ervan overigens waarschijnlijk een heel andere dan Sander Lestrade in zijn proefschrift voor woorden liet zien. Daar gaat het om de interne structuur van taal als een combinatie van de effecten van syntaxis en semantiek. Bij voornamen lijkt me dat niet aan de orde, en verwacht ik meer van sociaal bepaalde factoren.
Ik zal de frequentie van combinaties van beginletters van voornamen niet vergeten. De belangrijkste worden waarschijnlijk vooral bepaald door de traditionele topnamen.
Over de wet van Zipf schrijft u: “Daar gaat het om de interne structuur van taal als een combinatie van de effecten van syntaxis en semantiek.” Dat bedoel ik, wat betekent dit in gewone mensentaal en is dit niet meer een beschrijving , constatering dan een verklaring?
Sander Lestrade bewandelt die weg, en komt er ver mee. Een echte verklaring lijkt het me inderdaad niet, maar dat zou hij beter zelf kunnen uitleggen. Voor voornamen helpt het mij in ieder geval niet.