Taal en getal (1)
Om een taal goed te spreken, moet je een beetje kunnen tellen. Vaak lijkt dat tellen nogal simpel: voor het Nederlands volstaat het op het eerste gezicht vaak om het verschil te begrijpen tussen één en meer dan één, tussen enkel- en meervoud. Wie wil beweren dat hij Nederlands spreekt, zal het verschil moeten begrijpen tussen ‘een hond wandelt’ en ‘honden wandelen’.
In sommige talen zit het al ingewikkelder in elkaar. Die talen hebben behalve een enkelvoud en een meervoud ook bijvoorbeeld een dualis – die je alleen gebruikt voor groepjes van twee – en/of een paucalis – die je alleen gebruikt voor kleine groepjes tot een stuk of vier individuen.
Maar ook in een taal als het Nederlands is als nader beschouwd toch al snel ingewikkelder. Ik ben dezer dagen bij een workshop in Leiden waar taalkundigen, psychologen, neurologen en wiskundigen elkaar ontmoeten om over dit soort onderwerpen te praten. Het idee is dat je door talen nauwkeuriger te bestuderen meer kunt leren over het natuurlijke gevoel voor getallen dat wij mensen hebben.
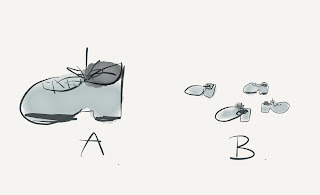
Ik heb al tijdens de eerste dag de interessantste dingen gehoord. Neem de drie plaatjes hieronder. Wanneer je mensen vraagt ‘wie heeft er meer schoenen’ bij het eerste plaatje, zegt iedereen: B.
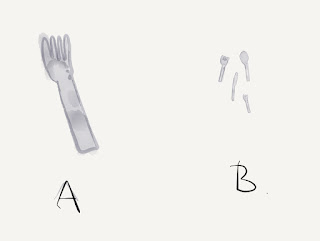
Datzelfde antwoord krijg je ook wanneer je mensen bij het volgende plaatje vraagt wie er het meeste bestek heeft:
Maar wanneer je nu vraagt wie er de meeste tandpasta heeft, is het antwoord ineens: A.
Wat is hier aan de hand? Bij schoenen en bestek is het antwoord te verkrijgen door tellen. Aan beide denken we op de een of andere manier als samengesteld: ofwel uit individuele schoenen, ofwel uit messen, vorken en lepels. Tandpasta zien we aan de andere kant niet als iets dat uit kleinste deeltjes (hoopjes tandpasta) bestaat, die we kunnen bekijken. Hier schatten we om de een of andere reden de totale hoeveelheid.
22 uur en 54 minuten
Fascinerend vind ik vooral ook het begrip ‘approximate number’ (benaderd getal) dat voor de meeste deelnemers van deze workshop kennelijk gesneden koek is. Wij mensen denken vaak in ‘benaderde’ getallen. Om dat te laten zien, toonde een van de deelnemers een Zwitsers verkeersbord dat aangaf dat er ‘over 103m’ een kruising was. Die 3 vinden we absurd; normaliter zeg je in zo’n geval 100m, en er is niemand die je hard valt om die paar meter.
Hoe en wanneer we afronden, hangt af van allerlei conventies. Een van de deelnemers hier, Manfred Krifka, liet zien dat als iemand zegt dat hij een artikel in 24 uur geschreven heeft, de meeste mensen nog steeds oké vinden als hij er 23 of 25 uur over heeft gedaan. Maar als iemand beweert een artikel in ’23 uur’ geschreven heeft, vinden we dat hij heeft gejokt als hij er feitelijk 24 uur aan heeft gewerkt. 24 uur is een eenheid en als je die noemt, ga je er bijna automatisch van uit dat dit wel ongeveer zal zijn bedoeld. Maar 23 uur betekent niets in ons idee van de wereld en kan dus alleen vrij letterlijk bedoeld zijn (al zal aan de andere kant niemand je op de minuut gaan afrekenen; dat doet men pas als je zegt dat je 22 uur en 54 minuten over hebt gedaan).
Bouwwerk
Krifka liet ook zien dat er in bijvoorbeeld Noorse teksten veel vaker over 50 (femti) wordt gesproken dan over 40 (førti) of 60 (seksti). In het Deens wordt er juist minder over 50 gesproken, wat waarschijnlijk te maken heeft met het feit dat men in die taal met een soort twintigtallig stelsel werkt, waarin 50 dus niet zo bijzonder is als in het tientallig stelsel, waarin 50 de helft is van 100 (40=fyre, 50=halvtreds, 60=tres).
Hoe mensen in alle talen en culturen kennelijk werken: hoe groter het getal, hoe minder nauwkeurig je hoeft te zijn. Wanneer ik zeg dat er 1000 mensen naar een concert kwamen, mag ik er best 50 naast zitten om nog steeds de waarheid te spreken, maar wanneer ik zeg dat er 100 mensen kwamen niet. Sterker nog, ook als ik zeg dat er ’90-100′ mensen waren, spreek ik nog steeds de waarheid als er bijvoorbeeld maar 88 kwamen opdagen.
Het wiskundige bouwwerk van de getallen is misschien gebouwd op de oerintuïties over hoeveelheden die in talen worden uitgedrukt, maar het is niet hetzelfde.

Heel interessant thema en wat een mooi programma! Ik ben een beetje jaloers dat ik er niet bij kan zijn. 🙂
"Tandpasta zien we aan de andere kant niet als iets dat uit kleinste deeltjes (hoopjes tandpasta) bestaat"
Inderdaad, maar als je vraagt "Wie heeft het meeste hoopjes tandpasta?" dan is het antwoord terug B, toch?
Tandpasta zien we eerst als een continue grootheid. Pas door er 'hoopjes' bij te zeggen signaleer dat je dat je moet tellen. Dit woord staat ook in het meervoud, net als 'schoenen' in de eerste vraag.
Eigenlijk vind ik zelf bestek het raarste geval van de drie, omdat het woord enkelvoud is en toch niet als continu gezien wordt. (Ik zou zelf "stukken bestek" gebruiken denk ik.)
We tellen tijd in het Nederlands vaak per kwartier(-tje). Maar in het Engels hoor ik vaker "twenty minutes". Hadden ze in Engeland andere klokken?
Mooi!
Is dit niet eigenlijk een kwestie van wat telbaar of niet telbaar is? Sommige zaken benoemen we als hoeveelheid (tandpasta, brood, geld…) en andere als aantallen (mensen, auto's, boeken).
Maar dit doet me meteen denken aan een verwant verschijnsel: het gebruik van 'een pak' en 'een stuk' om een toename of afname uit te drukken. Bijvoorbeeld: "morgen wordt het een stuk (of een pak?) warmer dan vandaag", of "er kwam een pak (of een stuk?) meer mensen kijken naar de voetbalmatch Ajax-PSV dan naar de ijshockeywedstrijd".
Op het eerste zicht lijkt 'stuk' meer geschikt voor niet-telbare hoeveelheden – een stuk warmer, een stuk duurder, een stuk kleiner – en 'pak' dus voor discrete aantallen – een pak minder toeschouwers, een pak minder kleren, een pak meer aardappelen.
Maar ik hoor op het VRT-nieuws wel vaker iets zeggen als "morgen wordt net een pak kouder." Dat lijkt me verkeerd. Maar ik weet het niet zo zeker…
Een derde komt niet zo vaak voor in het Engels, en ook in recepten vind je meestal geen referenties naar 1/3 lb of 1/3 pint. Maar inzake lengtematen heb je wel een foot die drie keer in een yard gaat, een mile die drie keer in een league gaat, en een inch die 12 (=4×3) keer in een foot gaat. Dat duodecimale perspectief bestond ook in de oude opdeling van het pond (12p in een shilling) en natuurlijk ook in de klok.
Diezelfde klok vind je natuurlijk overal, maar het 12-talig denken is toch een stuk meer courant in het Engels, misschien vandaar. (Overigens is het gebruik van 20 in tijdsbepalingen ook in Vlaanderen gebruikelijk – "over twintig minuten" is heel gewoon, en wij hebben het ook over "20 voor 2" in plaats van "10 over halftwee".
Ik vind het gebruik van een paar soms lastig. Het je het over een paar schoenen, dan zijn dat er twee, maar heb je het over een paar mensen, of een paar jaar geleden, dan kunnen dat er veel meer zijn. Soms kun je een paar dan beter vervangen door een aantal.
En een 12-tallig-stelsel is ontstaan omdat je 12 door meer getallen kan delen dan 10. 10 is alleen deelbaar door 2 en 5 en 12 door 2, 3, 4 en 6. Dat is handig in de handel, en zo kennen we nog het dozijn en het gros.
Ja, het heeft iets met telbaarheid te maken. Maar dat is zelf een lastig begrip. Rijst werkt bijvoorbeeld naar mijn gevoel als tandpasta, al kun je het in theorie tellen.
Ja, inderdaad: bestek is het vreemdste geval. Tijdens het programma werden ook nog 'rijst' tegenover 'bonen' genoemd. 'Rijst' moet je individueren om te kunnen tellen (rijstkorrels), maar bonen zie je kennelijk vanzelf al als individuele, telbare eenheden.
'Een paar' is nog lastiger: het heeft ook iets met de syntaxis te maken. Als je zegt dat 'een paar schoenen op de gang STAAT' zijn het er inderdaad twee, maar als 'een paar schoenen op de gang STAAN' zijn het er mogelijk ook meer dan twee. En dat geldt ook voor mensen: vergelijk 'een paar mensen STAAT te zoenen' tegenover 'een paar mensen STAAN te lummelen'.